Gaussian Splatting

开山论文：3D Gaussian Splatting for Real-Time Radiance Field Rendering

入门

3D GS的核心是一堆高斯点云，需要对点云的一些参数进行拟合

NeRF和$\alpha$混合的体积渲染：
颜色$C$是通过沿着射线的体积渲染得到的
$C=\sum\limits_{i=1}^{N}{T_i(1-\exp(-\sigma_i\delta_i))c_i}$
$T_i=\exp(-\sum\limits_{j=1}^{i-1}\sigma_i\delta_i)$
沿着间隔为$\delta$，采集射线上密度$\sigma$，透射率$T$和颜色$c$的样本，可以重写为:
$C=\sum\limits_{i=1}^{N}T_i\alpha_ic_i$
$\alpha_i=(1-\exp(-\sigma_i\delta_i))$ 和 $T_i=\prod\limits_{j=1}^{i-1}(1-\alpha_i)$
基于神经点的学习方法:
$C=\sum\limits_{i\in\mathcal{N}}c_i\alpha_i\prod\limits_{j=1}^{i-1}(1-\alpha_j)$
其中$\mathcal{N}$是N个与像素重叠的有序点，用以计算一个像素的颜色$C$，$c_i$是每个点的颜色，$\alpha_i$是通过计算协方差$\Sigma$的二维高斯分布乘以学习的每点不透明度给出的
区别：图像生成模型相同，但是渲染算法不同
- NeRF是一种隐式表示，是连续表示，随机抽样代价较大
- 点是一种结构化、离散的表示方式
  3D高斯是可微的，能够很容易投影到2D平米，允许快速$\alpha$混合渲染。

高斯函数(一维)：
$N_{\mu,\sigma}(x)=\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{(x-\mu)^2}{2\sigma^2})$
三维高斯函数：
$G_s(x)=(\frac{1}{\sqrt{2\pi}^3}\det{(\sum)})e^{-\frac{1}{2}(x-\mu)^T\sum^{-1}(x-\mu)}$
其中，$x=[a,b,c]^T$，$\mu$是椭球中心，协方差矩阵表示椭球在三轴上的伸缩和旋转，
$\sum=\begin{bmatrix}\sigma_a^2&Cov(a,b)&Cov(a,c)\Cov(b,a)&\sigma_b^2&Cov(b,c)\Cov(c,a)&Cov(c,b)&\sigma_c^2\end{bmatrix}$
协方差的特征向量就是椭球对称轴。

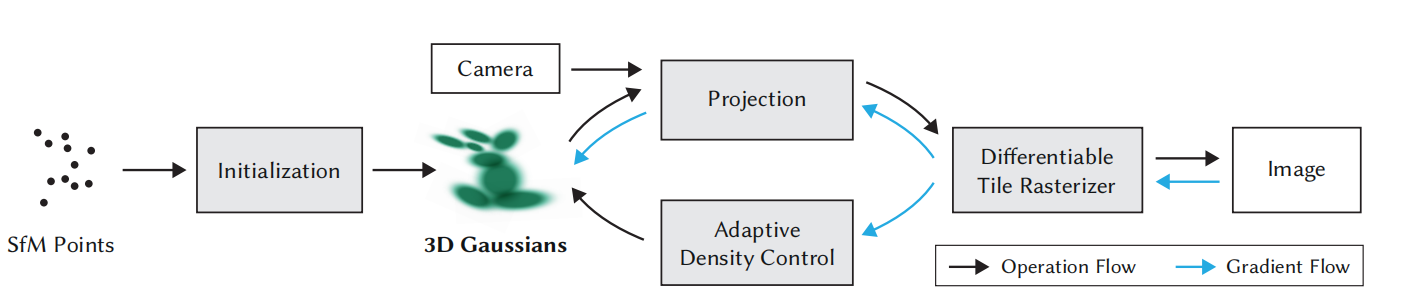
Word Flow

由输入，创建一组三维高斯分布，由位置($mean$)、协方差矩阵和不透明度($\alpha$)定义。
辐射场的各个方向的颜色由球谐波(Sphere Harmonics) 表示。
高斯函数：
$G(x)=e^{\frac{1}{2}(x)^T\sum^{-1}(x)}$
在$\alpha$混合中，这个高斯将与$\alpha$相乘，其中心点均值为$\mu$
3D向2D投影渲染，，给定观察变换$W$，相机坐标中的协方差矩阵为：
$\sum^{‘}=JW\sum W^TJ^T$
$J$是射影变换的仿射近似的雅可比矩阵。可以直接优化$\sum$来获得三维高斯分布，但协方差矩阵只有在正半定的时候才具有物理意义。使用梯度下降不能轻易约束地产生有效的矩阵，并且更新步骤和梯度可以很容易地创建无效的矩阵。
因此，使用更加直观的方法来进行处理。三维高斯分布的协方差$\sum$类似于描述椭球体的构型，给定一个比例矩阵$S$和旋转矩阵$R$，可以得到相应的$\sum$：
$\sum=RSS^TR^T$
为了独立优化，分别存储用于缩放的三维向量$s$和表示旋转的四元素$q$。
交叉优化的参数包括：
1. 点的三维位置$p$
2. 协方差矩阵$\sum$
3. 不透明度$\alpha$
4. 球谐函数
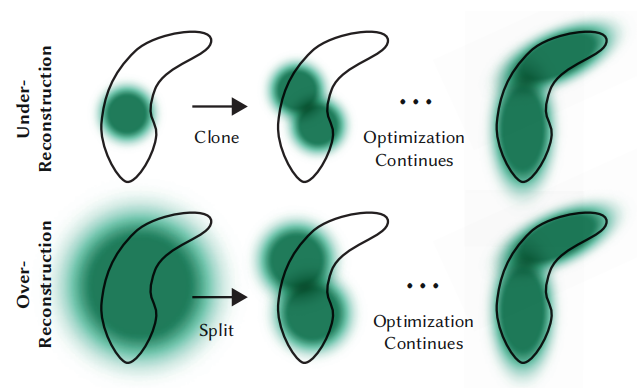
自适应控制：通过复制高斯点解决重建不足问题，通过分裂高斯点解决重建过度问题