FUEL探索

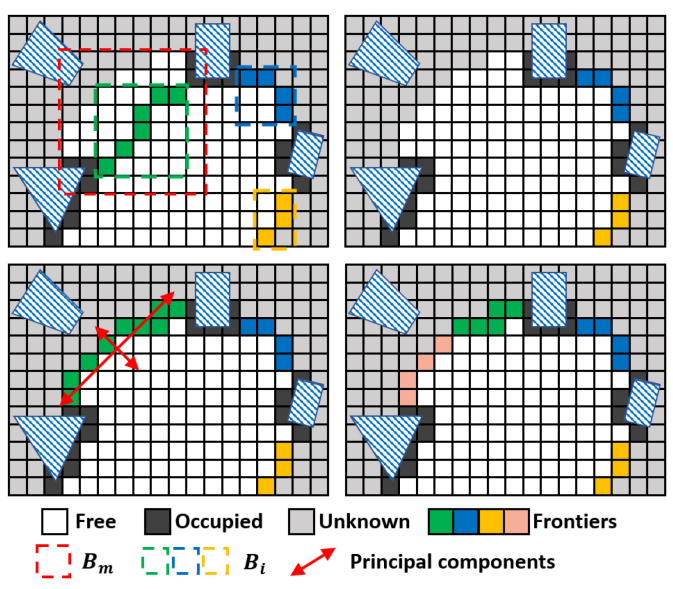
FIS结构

FUEL采用$FI_i$结构描述环境边界，包含的信息为：

• 边界聚类 $F_i$
• 所有数据这个类的网格 $C_i$
• $C_i$的中心位置 $p_{avg,i}$
• 边界框(AABB) $B_i$

主要步骤

1. 建立AABB框
2. 获取传感器信息，在新感知区域建立AABB框
3. 对比原有AABB框和新AABB框，删除不含边界的AABB框
4. 利用剩余的AABB框(FIS)更新边界
5. 判断AABB框对应边界大小，过大则主元分解
   

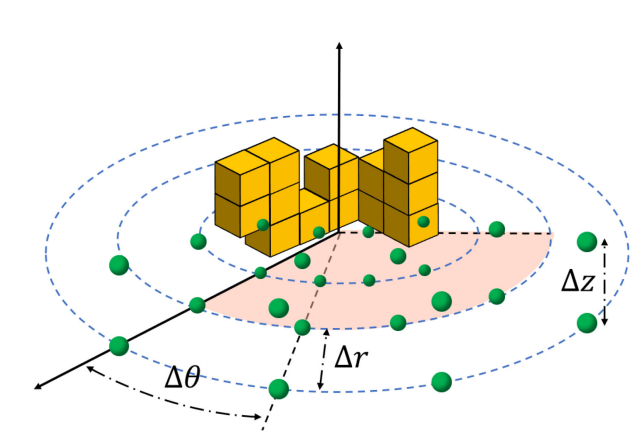
视点建立

对于每个FIS，建立视点，使用一个极坐标系，中心点在$C_i$的中心位置，在极坐标系内均匀采样，得到视点集合$VP_i$。

对每个$VP$，根据使覆盖范围最大来确定yaw角，覆盖范围计算使根据传感器模型，与已占用的栅格不冲突的边界栅格的数量。
并计算两个$VP$的最短时间：
$$t_{lb}(x_{k_1,j_1},x_{k_2,j_1})=\max{\frac{length(P(p_{k_1,j_1},p_{k_2,j_1}))}{v_{max}}，\frac{min(|\xi_{k_1,j_1}-\xi_{k2,j1}|,2\pi-|\xi_{k_1,j_1}-\xi_{k2,j1}|)}{\dot{\xi}_{max}}}$$
其中$P$是用A*算法规划的路径，前一项是位移速度限制，后一项是角速度限制。

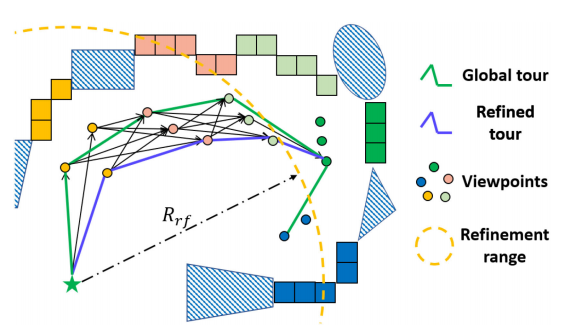
全局规划

TSP问题，寻找开环回路，假设有$N_{cls}$个类，$M_{tsp}$代表${N_{cls}+1}$维矩阵，主要部分为${N_{cls}\times N_{cls}}$块，则TSP问题为：
$$M_{tsp}(k_1,k_2)=M_{tsp}(k_2,k_1)=t_{lb}(x_{k_1,1},x_{k_2,1}),k_1,k_2\in {1,2,…,N_{cls}}$$
$$M_{tsp}(0,k)=t_{lb}(x_{0,1},x_{k,1})+\omega_c\cdot c_c(x_{k,1}),k\in {1,2,…,N_{cls}}$$
其中$c_c(x_{k,1})$是运动一致性成本，用来惩罚运动方向改变。
$$c_c(x_{k,1})=cos^{-1}\frac{(p_{k,j}-p_0)\cdot v_0}{||p_{k,j}-p_0||\space ||v_0||}$$
最后，通过$M_{tsp}(k,0)=0,k\in {1,2,…,N_{cls}}$，将开环TSP问题转化为闭环问题求解，且不会引入额外的cost。

局部规划

全局规划只是找到了访问所有聚类的最佳顺序，但是只涉及每个类都单个视点，不一定是所有视点中的最佳组合。
因此，在局部路径规划中，以当前位置做一个半径圆，在该圆内同时再取一些其他的视点，将这些在半径中的视点进行全连接，然后通过dijkstra算法寻找最优路径$E={x_{1,j_1},x_{2,j_2},…,x_{N_{rf},j_{N_{rf}}}}$。
$$c_{rf}(E)=t_{lb}(x_0,x_{1,j_1})+\omega_c\cdot c_c(x_{1,j_1})+t_{lb}(x_{N_{rf}+1,1})+\sum_{k=1}^{N_{rf}-1}t_{lb}(x_{k,j_k},x_{k+1,j_{k+1}})$$