对极几何

DUSt3R

DUSt3R在描述相对位姿估计都时候提到

One way is to perform 2D matching and recover intrinsics as described above, then estimate the Epipolar matrix and recover the relative pose

相对位姿估计的一种方法是执行2D匹配并恢复如上所述的内部函数，然后估计极线矩阵并恢复相对姿态，另一种方法是直接比较点地图。当然，DUSt3R采用的是后者。

对极几何

考虑如下场景：

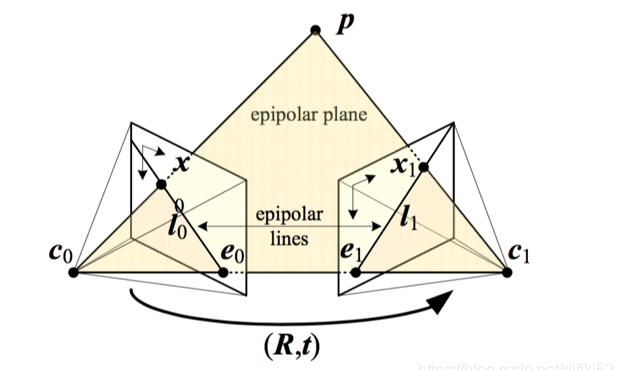
主要思想是：

1. 给定两张影像，获得对应的3D坐标点对。
2. 先计算基础矩阵F，
3. 然后结合相机内参矩阵K，恢复本质矩阵E。
4. 对E进行SVD分解，得到R和t。

对极约束

假设世界坐标系下点坐标为$P$，像素坐标系下点坐标为$p$，相机内参矩阵为$K$，相机外参矩阵为$R, t$，则有：
$$dp=KP$$
其中$d$为齐次化矩阵，对于两个相机，有：
$$d_0p_0=KP$$
$$d_1p_1=KP$$
已知$R, t$，则有：
$$d_1p_1=K(RP+t)$$
令$x=K^{-1}p$，则有：
$$d_0x_0=P$$
$$d_1x_1=RP+t$$
即：
$$d_1x_1=R(d_0x_0)+t$$
两边同时叉乘$t$，有：
$$t\times d_1x_1=t\times R(d_0x_0)$$
$$t\times x_1=t\times Rx_0$$
两边同时左乘$x^T_1$，有：
$$x^T_1t\times x_1=x^T_1t\times Rx_0$$
得到：
$$0=x^T_1t\times R^Tx_0$$

本征矩阵

由对极约束，本征矩阵$E$满足：
$$E=t\times R$$
$$x^T_1Ex_0=0$$
多组点可以求得$E$，然后对$E$进行SVD分解，得到$R, t$。

基础矩阵

基础矩阵$F$满足：
$$F=K^{-T}EK^{-1}$$
是在本征矩阵基础上加入了相机内参矩阵的约束。

其他

1. 通过对极几何可以恢复相机的相对姿态，但是无法恢复绝对姿态。