DUSt3R

DUST3r

github连接：DUSt3R

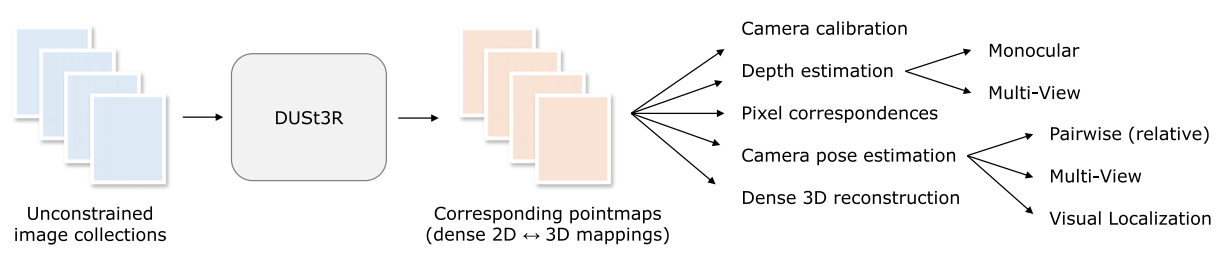
DUSt3R是一种旨在简化几何3D视觉任务的新框架。作者着重于使3D重建过程更加易于使用和高效。该框架利用深度学习和几何处理的最新进展，提高了准确性并降低了计算复杂性。

DUSt3R以一组不受约束的图像为输入，输出点图(pointmaps)，从这些点图可以直接推导出各种几何量。

算法流程

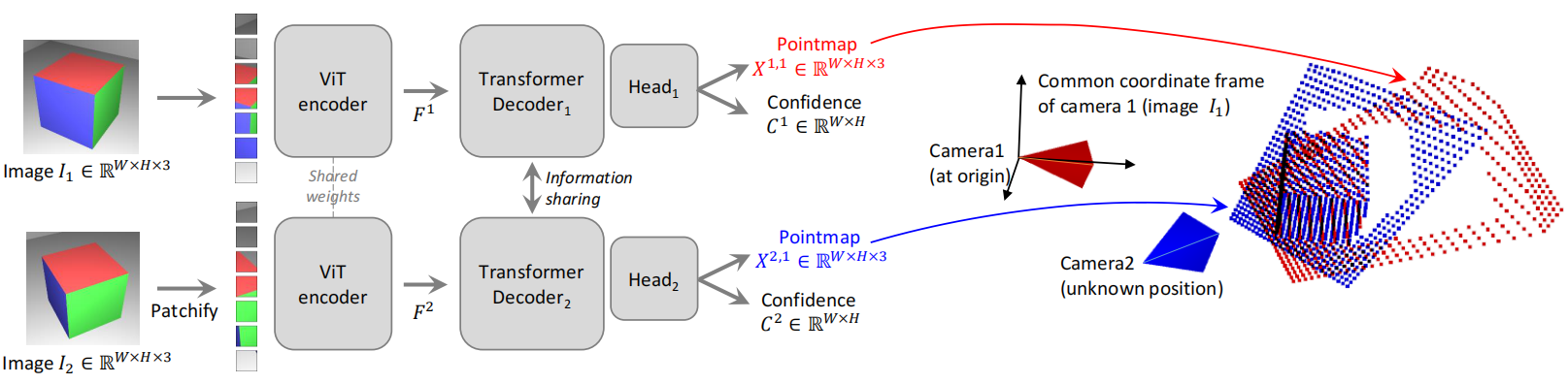
网络结构

输入： 两张不受约束的图像

通过共享权重的ViT网络生成两个token，返回在解码器中进行联合推理，在解码器传递过程中，两个分支之间不断共享信息。这对于输出正确对齐的点图至关重要。也就是说，每个解码器块关注来自另一个分支的token：

$$G_i^1 = DecoderBlock_i^1 (G^1_{i-1}, G^2_{i-1})$$

$$G_i^2 = DecoderBlock_i^2 (G^2_{i-1}, G^1_{i-1})$$

输出： 经过Head处理后输出点云图和置信图，点云图的坐标系为第一张图片的坐标系。

训练目标

1. 3D回归损失函数

   $$\mathcal{l}_{regr}(v, i)=||\frac{1}{z}X_i^{v,1}-\frac{1}{\overline{z}}\overline{X}_i^{v,1}||$$

   $X^{n,m}$是指相机$n$得到的点云图$X^n$在相机$m$的坐标系下观测到的。上述公式用于计算像素$i\in D^v$在视图$v$中的3D回归损失。

   $$\overline{z}=norm(X^1,X^2) = \frac{1}{|D^1|+|D^2|}\sum_{v\in{1,2}}\sum_{i\in D^v}||X_i^v||$$

   代表平均距离，分别通过$z$和$\overline{z}$对预测和真实点图进行归一化，它们只是表示所有有效的点到原点的平均距离。

2. 置信度感知损失
   存在定义不明确的 3D 点，例如在天空中或半透明物体上。更一般地，图像中的某些部分通常比其他部分更难预测。因此，共同学习预测每个像素的分数，该分数表示网络对该特定像素的置信度。最终的训练目标是所有有效像素的置信度加权回归损失：

   $$\mathcal{L}_{conf}=\sum_{v\in{1,2}}\sum_{i\in D^v}\mathcal{C}_i^{v,1}\mathcal{l}_{regr}(v, i)-\alpha\log{C_i^{v,1}}$$

下游应用

1. 点匹配
   通过最近邻算法，建立两个图像像素之间的对应关系。
2. 恢复相机内参
   假设主点大致位于中心，像素为正方形，因此只需估计焦点$f$。
3. 相对姿态估计
   执行 2D 匹配并恢复内参矩阵，然后估计对极矩阵并恢复相对姿态；或者使用 Procrustes 对齐比较点图获得相对姿态
   参考我的另一篇文章对极几何
4. 绝对姿态估计

全局对齐

1. 配对图
   俩俩配对，构建一个连通图，根据两对的平均置信度测量它们的重叠，然后过滤掉低置信度的对。
2. 全局优化
3. 恢复相机参数