建立搜索算法完成从任意初始状态向目标状态的操作转换
二阶魔方示意图如下:

问题定义
将二阶魔方展开如下图

其中l1,l2,...,l12均为二维矩阵,代表所在行的两个方块颜色。
我们使用1至6代表六种不同的颜色,则还原后的展开图表达式为:
[[l1,l2],[l3,l4],...,[l11,l12]]=[[11,11],[22,22],...,[66,66]]
操作定义
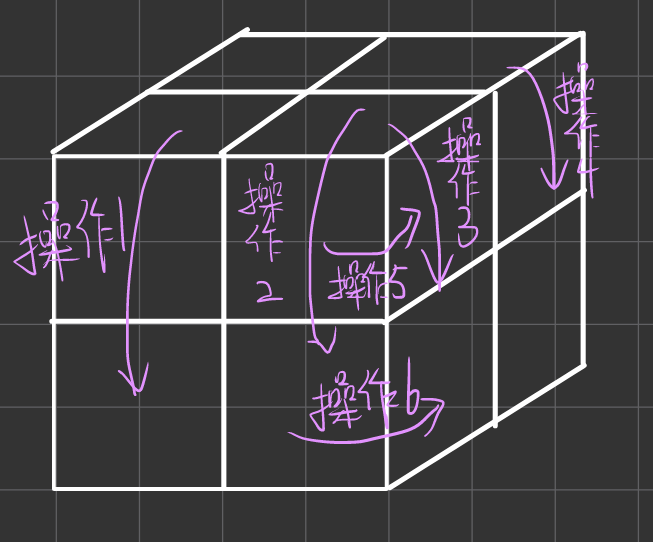
我们定义6种操作方法,可以完成魔方的任意自由度地旋转,具有空间完备性,其实3种操作足以还原魔方,但是可能结果不是最优解,也可以定义12种操作方式,但是这12种操作方式包含了6种冗余操作,除了增加编程难度以外没有任何好处
下面展示这六种操作:
算法实现
涉及算法:
BFS
广度优先搜索,又称宽搜,信竞基础,不多介绍
递归
函数自己调用自己,信竞基础,不多介绍
好了,可以愉快敲代码了
代码很简单,但是贼难敲,且费脑细胞
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
|
#include <iostream>
#include <queue>
#include <cmath>
#include <algorithm>
using namespace std;
struct magic_cube{
int a[13][3];
queue<int> steps;
}init;
queue<magic_cube> q;
bool flag = 0;
void input_cube() {
cout<<"input cube: "<<endl;
for (int i=1; i<=12; i++) {
for (int j=1; j<=2; j++)
cin>>init.a[i][j];
}
}
bool is_back(magic_cube t) {
if (t.a[1][1] == t.a[1][2] && t.a[1][1] == t.a[2][1] && t.a[1][1] == t.a[2][2] &&
t.a[3][1] == t.a[3][2] && t.a[3][1] == t.a[4][1] && t.a[3][1] == t.a[4][2] &&
t.a[5][1] == t.a[5][2] && t.a[5][1] == t.a[6][1] && t.a[5][1] == t.a[6][2] &&
t.a[7][1] == t.a[7][2] && t.a[7][1] == t.a[8][1] && t.a[7][1] == t.a[8][2] &&
t.a[9][1] == t.a[9][2] && t.a[9][1] == t.a[10][1] && t.a[9][1] == t.a[10][2] &&
t.a[11][1] == t.a[11][2] && t.a[11][1] == t.a[12][1] && t.a[11][1] == t.a[12][2])
return true;
else return false;
}
void act_1(magic_cube t) {
magic_cube tmp;
tmp = t;
tmp.a[5][1] = t.a[1][1];
tmp.a[6][1] = t.a[2][1];
tmp.a[1][1] = t.a[10][2];
tmp.a[2][1] = t.a[9][2];
tmp.a[11][1] = t.a[5][1];
tmp.a[12][1] = t.a[6][1];
tmp.a[10][2] = t.a[11][1];
tmp.a[9][2] = t.a[12][1];
tmp.a[3][1] = t.a[4][1];
tmp.a[3][2] = t.a[3][1];
tmp.a[4][1] = t.a[4][2];
tmp.a[4][2] = t.a[3][2];
tmp.steps.push(1);
if(is_back(tmp)) {
flag = 1;
cout<<tmp.steps.size()<<endl;
cout<<"steps: "<<endl;
while (!tmp.steps.empty()){
cout<<tmp.steps.front()<<endl;
tmp.steps.pop();
}
}
q.push(tmp);
}
void act_2(magic_cube t) {
magic_cube tmp;
tmp = t;
tmp.a[5][2] = t.a[1][2];
tmp.a[6][2] = t.a[2][2];
tmp.a[1][2] = t.a[10][1];
tmp.a[2][2] = t.a[9][1];
tmp.a[11][2] = t.a[5][2];
tmp.a[12][2] = t.a[6][2];
tmp.a[10][1] = t.a[11][2];
tmp.a[9][1] = t.a[12][2];
tmp.a[7][1] = t.a[7][2];
tmp.a[7][2] = t.a[8][2];
tmp.a[8][1] = t.a[7][1];
tmp.a[8][2] = t.a[8][1];
tmp.steps.push(2);
if(is_back(tmp)) {
flag = 1;
cout<<tmp.steps.size()<<endl;
cout<<"steps: "<<endl;
while (!tmp.steps.empty()){
cout<<tmp.steps.front()<<endl;
tmp.steps.pop();
}
}
q.push(tmp);
}
void act_3(magic_cube t) {
magic_cube tmp;
tmp = t;
tmp.a[2][1] = t.a[4][2];
tmp.a[2][2] = t.a[3][2];
tmp.a[3][2] = t.a[11][1];
tmp.a[4][2] = t.a[11][2];
tmp.a[11][1] = t.a[8][1];
tmp.a[11][2] = t.a[7][1];
tmp.a[8][1] = t.a[2][2];
tmp.a[7][1] = t.a[2][1];
tmp.a[5][2] = tmp.a[5][1];
tmp.a[5][1] = tmp.a[6][1];
tmp.a[6][1] = tmp.a[6][2];
tmp.a[6][2] = tmp.a[5][2];
tmp.steps.push(3);
if(is_back(tmp)) {
flag = 1;
cout<<tmp.steps.size()<<endl;
cout<<"steps: "<<endl;
while (!tmp.steps.empty()){
cout<<tmp.steps.front()<<endl;
tmp.steps.pop();
}
}
q.push(tmp);
}
void act_4(magic_cube t) {
magic_cube tmp;
tmp = t;
tmp.a[1][1] = t.a[4][1];
tmp.a[1][2] = t.a[3][1];
tmp.a[3][1] = t.a[12][1];
tmp.a[4][1] = t.a[12][2];
tmp.a[12][1] = t.a[8][2];
tmp.a[12][2] = t.a[7][2];
tmp.a[8][2] = t.a[1][2];
tmp.a[7][2] = t.a[1][1];
tmp.a[9][1] = tmp.a[9][2];
tmp.a[9][2] = tmp.a[10][2];
tmp.a[10][2] = tmp.a[10][1];
tmp.a[10][1] = tmp.a[9][1];
tmp.steps.push(4);
if(is_back(tmp)) {
flag = 1;
cout<<tmp.steps.size()<<endl;
cout<<"steps: "<<endl;
while (!tmp.steps.empty()){
cout<<tmp.steps.front()<<endl;
tmp.steps.pop();
}
}
q.push(tmp);
}
void act_5(magic_cube t) {
magic_cube tmp;
tmp = t;
tmp.a[5][2] = t.a[3][2];
tmp.a[5][1] = t.a[3][1];
tmp.a[3][1] = t.a[9][1];
tmp.a[3][2] = t.a[9][2];
tmp.a[9][1] = t.a[7][1];
tmp.a[9][2] = t.a[7][2];
tmp.a[7][1] = t.a[5][1];
tmp.a[7][2] = t.a[5][2];
tmp.a[1][1] = t.a[1][2];
tmp.a[1][2] = t.a[2][2];
tmp.a[2][2] = t.a[2][1];
tmp.a[2][1] = t.a[1][1];
tmp.steps.push(5);
if(is_back(tmp)) {
flag = 1;
cout<<tmp.steps.size()<<endl;
cout<<"steps: "<<endl;
while (!tmp.steps.empty()){
cout<<tmp.steps.front()<<endl;
tmp.steps.pop();
}
}
q.push(tmp);
}
void act_6(magic_cube t) {
magic_cube tmp;
tmp = t;
tmp.a[6][2] = t.a[4][2];
tmp.a[6][1] = t.a[4][1];
tmp.a[4][1] = t.a[10][1];
tmp.a[4][2] = t.a[10][2];
tmp.a[10][1] = t.a[8][1];
tmp.a[10][2] = t.a[8][2];
tmp.a[8][1] = t.a[6][1];
tmp.a[8][2] = t.a[6][2];
tmp.a[11][1] = t.a[12][1];
tmp.a[11][2] = t.a[11][1];
tmp.a[12][2] = t.a[11][2];
tmp.a[12][1] = t.a[12][2];
tmp.steps.push(6);
if(is_back(tmp)) {
flag = 1;
cout<<tmp.steps.size()<<endl;
cout<<"steps: "<<endl;
while (!tmp.steps.empty()){
cout<<tmp.steps.front()<<endl;
tmp.steps.pop();
}
}
q.push(tmp);
}
void search(magic_cube t, int num) {
switch(num) {
case 1: act_1(t); break;
case 2: act_2(t); break;
case 3: act_3(t); break;
case 4: act_4(t); break;
case 5: act_5(t); break;
case 6: act_6(t); break;
default: break;
}
}
void find_best() {
if(flag) return;
search(q.front(), 1);
search(q.front(), 2);
search(q.front(), 3);
search(q.front(), 4);
search(q.front(), 5);
search(q.front(), 6);
q.pop();
find_best();
}
int main() {
input_cube();
q.push(init);
find_best();
}
|
测试样例:
5 1 5 1 2 2 2 2 1 3 1 3 4 4 4 4 5 6 5 6 3 6 3 6
显然,只需要拧一下就可以复原
输出:
input cube:
1
steps:
2
第一行代表总的操作次数,第二行代表从第一次操作开始的所有操作编号



